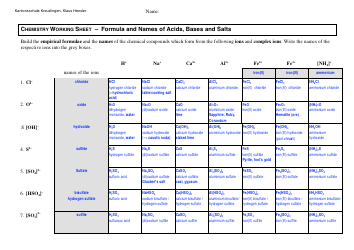
Countable and Uncountable Sets Cheat Sheet - Rich Schwartz

The document "Countable and Uncountable Sets Cheat Sheet" by Rich Schwartz is a resource for mathematics students or enthusiasts who want to understand and distinguish between countable and uncountable sets. It provides a concise summary of the key concepts and properties related to these types of sets.

FAQ

Q: What is a countable set?
A: A countable set is a set that can be put into a one-to-one correspondence with the natural numbers (0, 1, 2, 3, ...).

Q: What is an uncountable set?
A: An uncountable set is a set that cannot be put into a one-to-one correspondence with the natural numbers. Examples include the set of all real numbers and the set of all points on a line.

Q: What is a one-to-one correspondence?
A: A one-to-one correspondence, also known as a bijection, is a function that assigns each element of one set to a unique element in another set, and vice versa.

Q: Can a countable set be infinite?
A: Yes, a countable set can be infinite. For example, the set of all natural numbers is countable and infinite.

Q: Is the set of all real numbers countable?
A: No, the set of all real numbers is uncountable.

Q: Are there more elements in a countable set or an uncountable set?
A: There are more elements in an uncountable set. Countable sets are generally considered to have fewer elements than uncountable sets.

Q: What are some examples of countable sets?
A: Examples of countable sets include the set of all natural numbers, the set of all integers, and the set of all rational numbers.

Q: What are some examples of uncountable sets?
A: Examples of uncountable sets include the set of all real numbers, the set of all points on a line, and the set of all irrational numbers.

Q: Can an uncountable set have a countable subset?
A: Yes, an uncountable set can have a countable subset. For example, the set of all rational numbers is countable and is a subset of the uncountable set of all real numbers.