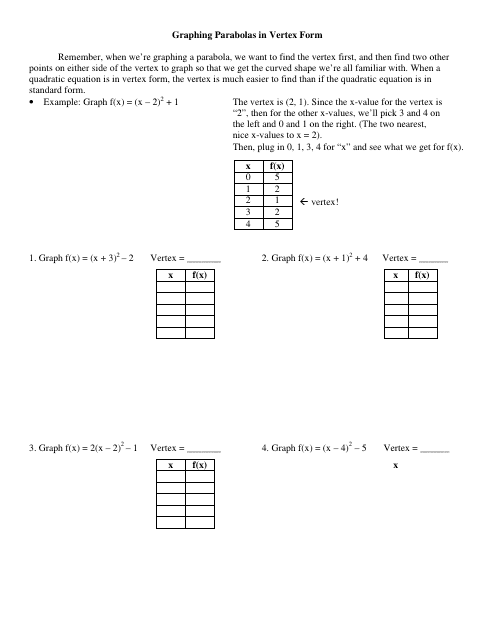
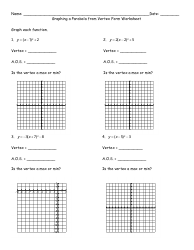
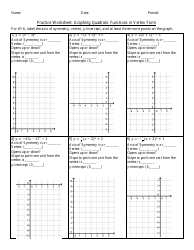
Graphing Parabolas in Vertex Form Worksheet

The Graphing Parabolas in Vertex Form Worksheet is used as a practice tool to help students understand and master the concept of graphing parabolas in vertex form. It provides exercises and problems for students to practice and apply their knowledge of this topic.

FAQ

Q: What is vertex form?
A: Vertex form is a way to write the equation of a parabola in the form y = a(x-h)^2 + k, where (h,k) represents the vertex.

Q: How do I graph a parabola in vertex form?
A: To graph a parabola in vertex form, start by plotting the vertex (h,k). Then, use the symmetry of the parabola to plot additional points on either side. Finally, draw a smooth curve through the plotted points.

Q: What does 'a' represent in vertex form?
A: 'a' represents the coefficient in front of the (x-h)^2 term. It determines whether the parabola opens upwards or downwards.

Q: How do I find the vertex of a parabola in vertex form?
A: The vertex of a parabola in vertex form is given by the coordinates (h,k), where h is the x-coordinate of the vertex and k is the y-coordinate of the vertex.

Q: Can a parabola in vertex form open sideways?
A: No, a parabola in vertex form can only open upwards or downwards. If a parabola opens sideways, it is not in vertex form.

Q: What is the axis of symmetry for a parabola in vertex form?
A: The axis of symmetry for a parabola in vertex form is a vertical line passing through the vertex. It has the equation x = h, where h is the x-coordinate of the vertex.