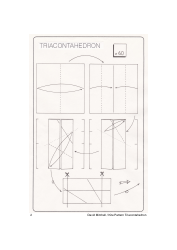
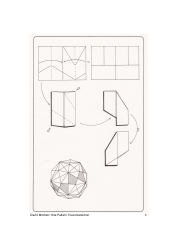
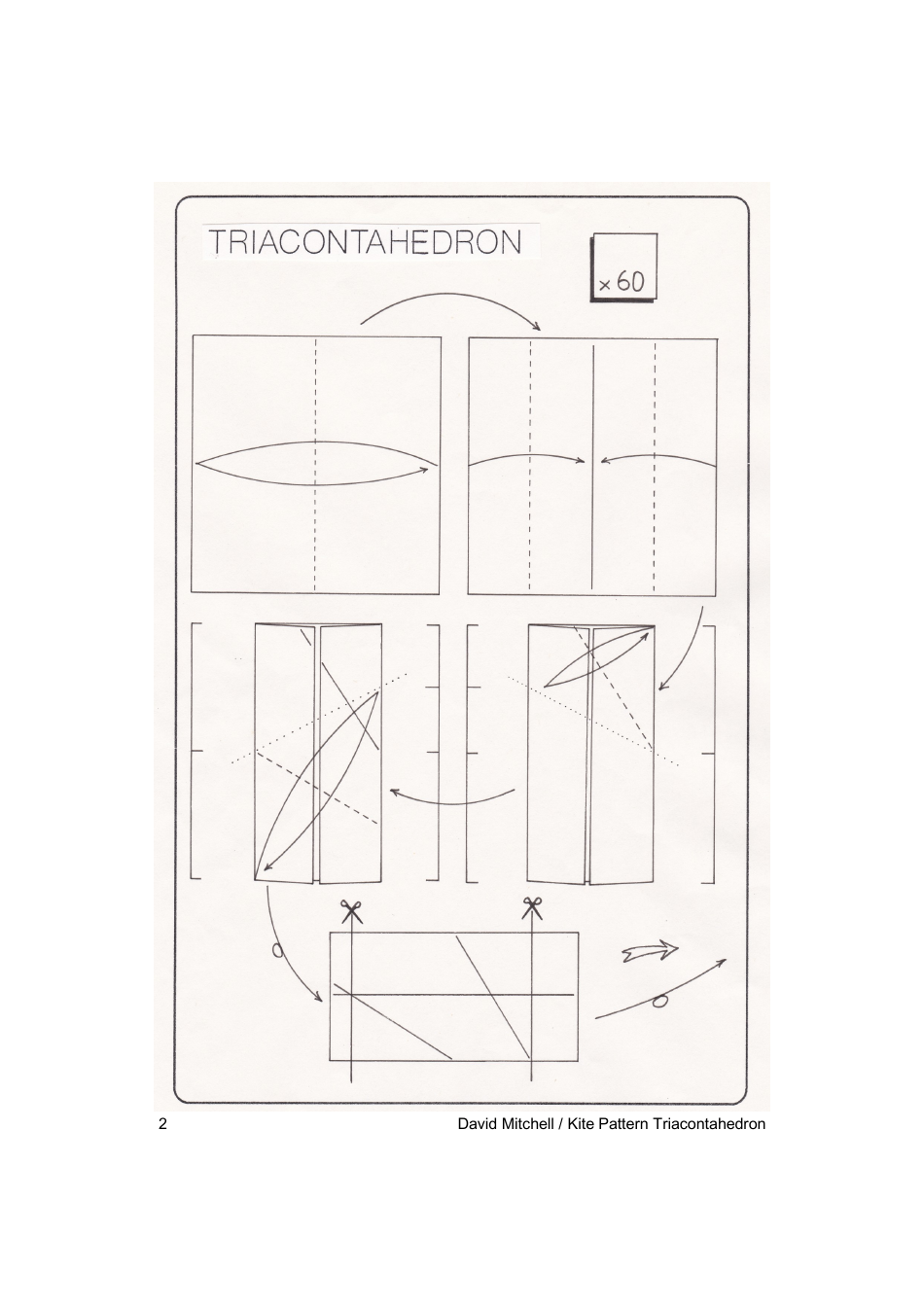
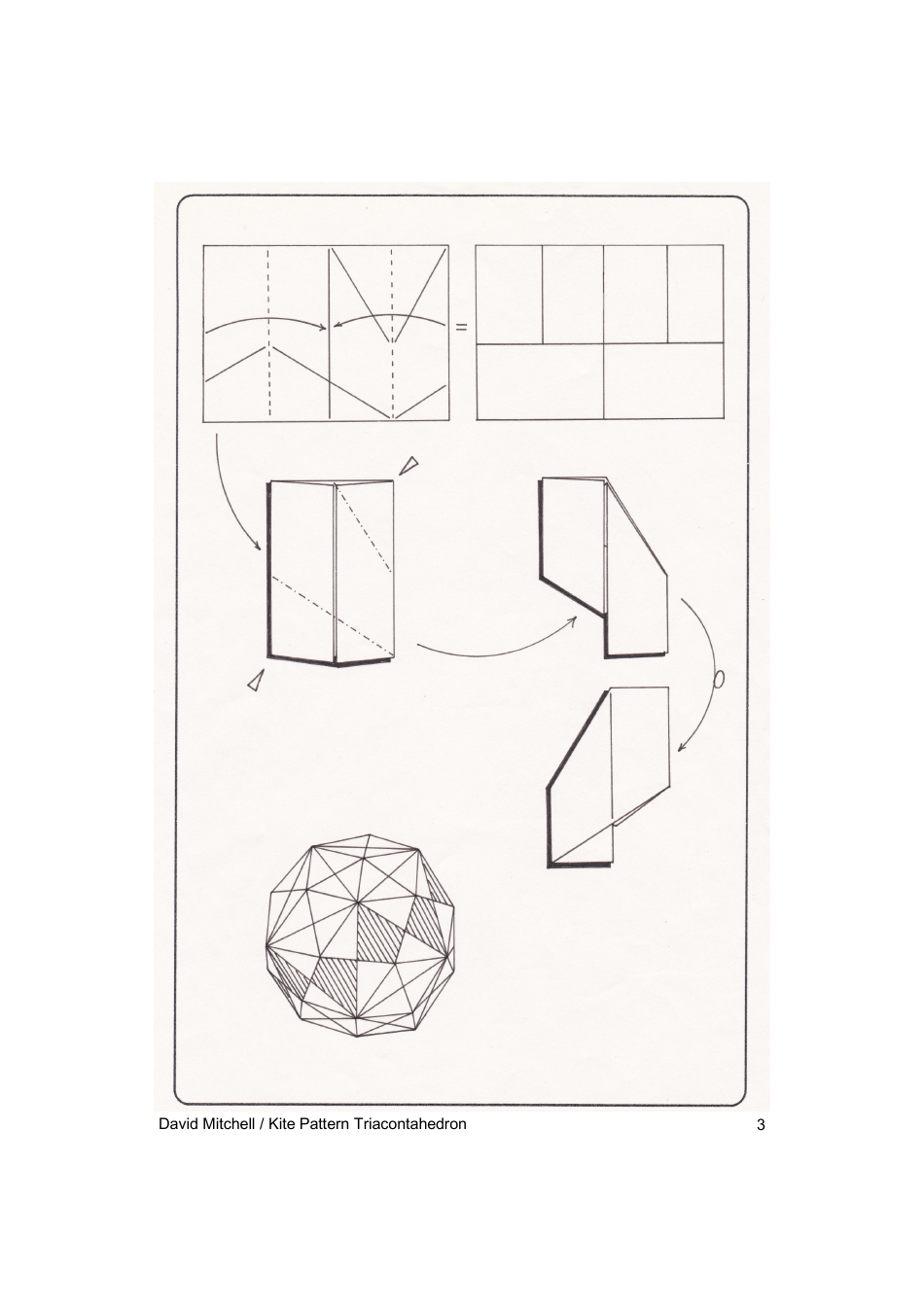
Kite Pattern Triacontahedron Guide

The Kite Pattern Triacontahedron Guide, if such a document exists, would potentially be a step-by-step guide or instructional manual related to the craft of creating a kite pattern on a triacontahedron shaped object. A triacontahedron is a polyhedron with 30 faces. However, such a specific document might not exist, as the topic is rather unique and niche. As a document knowledge system, I cannot find any specific recorded document titled "Kite Pattern Triacontahedron Guide".

FAQ

Q: What is a Kite Pattern Triacontahedron?
A: A Kite Pattern Triacontahedron is a geometric shape that is a part of polyhedral structures. This shape is a 30-sided polygon or polyhedron. Each of its faces is a kite-like shape, which gives it the name.

Q: What are some common uses of a Kite Pattern Triacontahedron?
A: The Kite Pattern Triacontahedron is often used in fields where complex geometrical shapes are needed, such as architecture, structural design, and 3D modelling. It can also be used in arts and crafts for making intricate paper models

Q: How can one create a Kite Pattern Triacontahedron?
A: A Kite Pattern Triacontahedron can be created using specific techniques of origami, fittings, or 3D modelling software. The procedure includes creating a kite-shaped pattern and then replicating and assembling it to form a 30-sided geometric figure.

Q: What are some examples of Kite Pattern Triacontahedron in real life?
A: Real-life examples of kite pattern triacontahedrons might be not common, as they are mainly used in abstract geometry. However, some intricate architectural structures, craft models, or even some types of jewelry may implement a similar design approach.

Q: What are the characteristics of a Kite Pattern Triacontahedron?
A: A Kite Pattern Triacontahedron features thirty faces, all of which have a 'kite' shape. The overall shape is symmetrical, and each face commonly has two different lengths for the edges, longer and shorter, forming a 'kite'.

Q: What is the relation of Triacontahedron to other polyhedrons?
A: Polyhedrons like Triacontahedron falls under the category of zonohedra, a type of polyhedra with faces that are parallelograms or rectangles (zonogons). Triacontahedron specifically is dual to the icosidodecahedron, means it shares the same vertices as an icosidodecahedron.