Sequences and Series Cheat Sheet

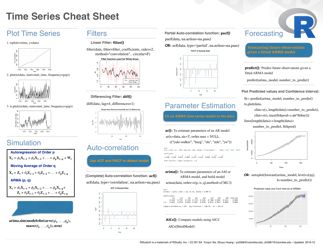
The Sequences and Series Cheat Sheet is a document that provides a concise summary of key concepts, formulas, and techniques related to sequences and series in mathematics. It is designed to assist students or learners in understanding and applying these mathematical concepts.

FAQ

Q: What is a sequence?
A: A sequence is a list of numbers in a specific order.

Q: What is a series?
A: A series is the sum of the terms in a sequence.

Q: What is an arithmetic sequence?
A: An arithmetic sequence is a sequence where the difference between consecutive terms is constant.

Q: What is the formula for the nth term of an arithmetic sequence?
A: The formula for the nth term of an arithmetic sequence is an = a1 + (n - 1)d, where a1 is the first term and d is the common difference.

Q: What is a geometric sequence?
A: A geometric sequence is a sequence where the ratio of consecutive terms is constant.

Q: What is the formula for the nth term of a geometric sequence?
A: The formula for the nth term of a geometric sequence is an = a1 * r^(n - 1), where a1 is the first term and r is the common ratio.

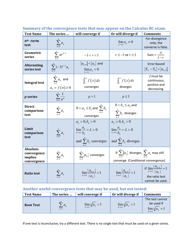
Q: What is a finite series?
A: A finite series is a series with a limited number of terms.

Q: What is an infinite series?
A: An infinite series is a series with an unlimited number of terms.

Q: What is the formula for the sum of an arithmetic series?
A: The formula for the sum of an arithmetic series is S = (n/2)(a1 + an), where S is the sum, n is the number of terms, a1 is the first term, and an is the last term.

Q: What is the formula for the sum of a geometric series?
A: The formula for the sum of a geometric series is S = a1 * (1 - r^n)/(1 - r), where S is the sum, a1 is the first term, r is the common ratio, and n is the number of terms.