Convergence Tests for Series Cheat Sheet

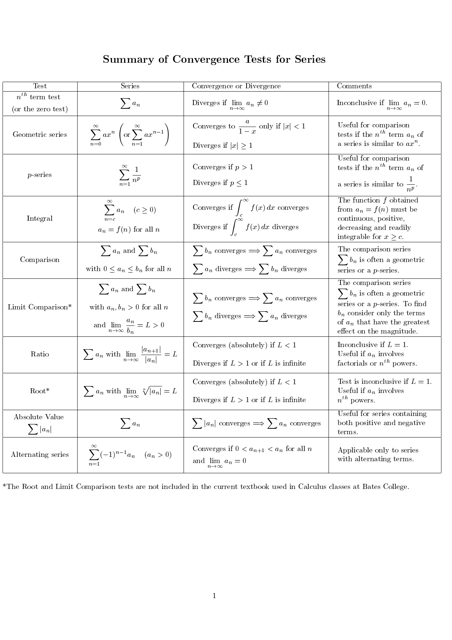
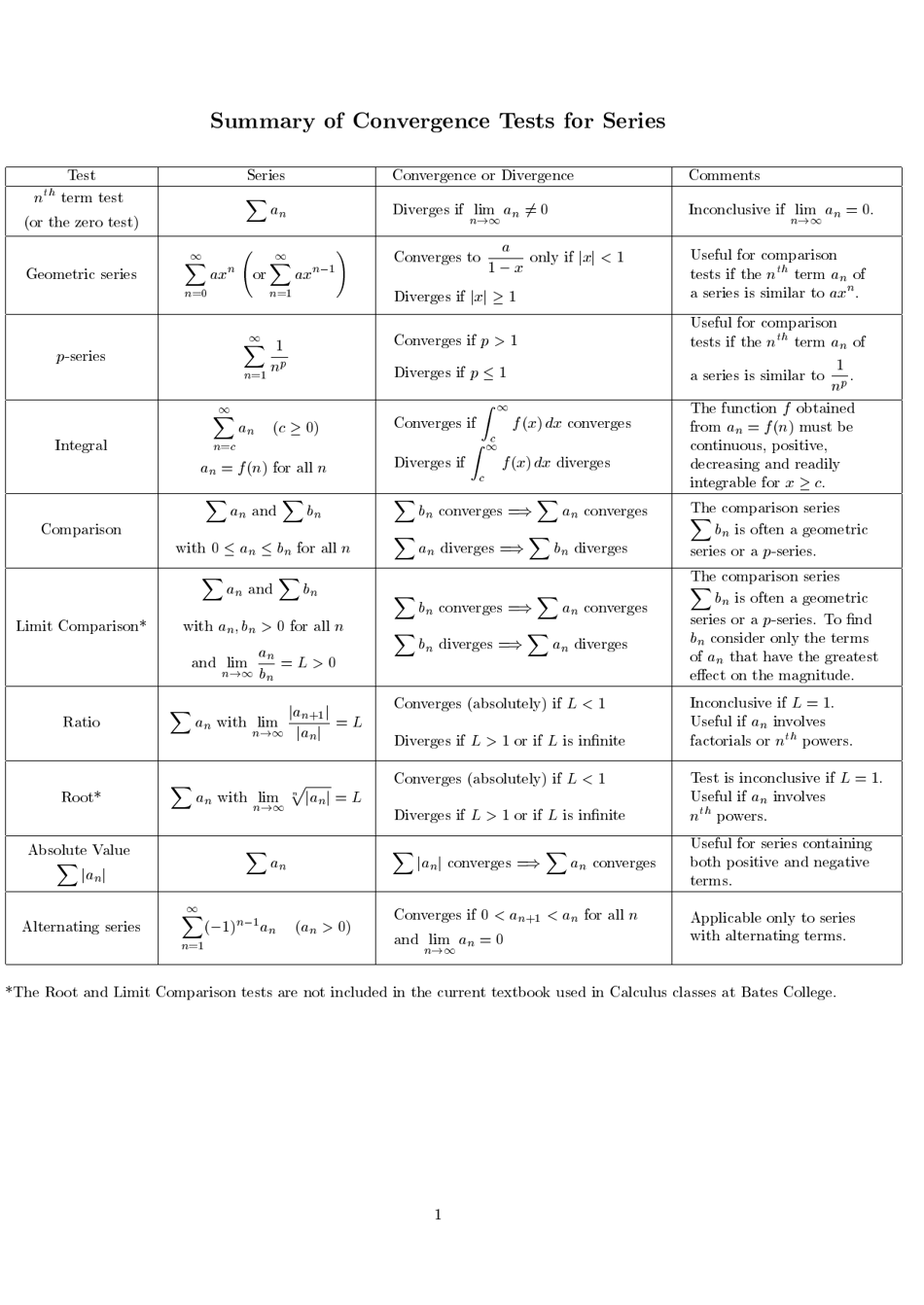
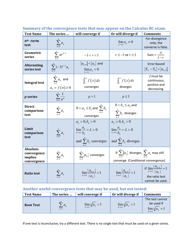
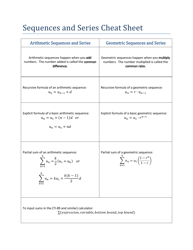
The Convergence Tests for Series Cheat Sheet is a document that provides a summary or quick reference guide for various techniques used to determine the convergence or divergence of infinite series in mathematics. It includes helpful formulas and rules to analyze different types of series.

FAQ

Q: What is a convergent series?
A: A series is said to be convergent if the sum of its terms approaches a finite value.

Q: What is a divergent series?
A: A series is said to be divergent if the sum of its terms does not approach a finite value.

Q: What is the Comparison Test?
A: The Comparison Test states that if the terms of a series can be compared to the terms of a known convergent or divergent series, then the original series will have the same convergence or divergence.

Q: What is the Limit Comparison Test?
A: The Limit Comparison Test is a variation of the Comparison Test that uses the limit of the ratio of the terms of two series to determine convergence or divergence.

Q: What is the Ratio Test?
A: The Ratio Test is a test for convergence that uses the limit of the ratio of consecutive terms of a series to determine if the series converges or diverges.

Q: What is the Root Test?
A: The Root Test is a test for convergence that uses the limit of the nth root of the absolute value of the terms of a series to determine convergence or divergence.

Q: What is the Alternating Series Test?
A: The Alternating Series Test is a test for convergence that applies to alternating series, where the signs of the terms alternate between positive and negative.

Q: What is the Absolute Convergence Test?
A: The Absolute Convergence Test states that if the absolute value of the terms of a series converge, then the series itself converges.

Q: What is the Conditional Convergence Test?
A: The Conditional Convergence Test states that if the terms of a series converge but the absolute values of the terms do not, then the series converges conditionally.

Q: What is the Divergence Test?
A: The Divergence Test states that if the terms of a series do not converge to zero, then the series must diverge.