Calculus Bc Exam Series Convergence Tests Cheat Sheet

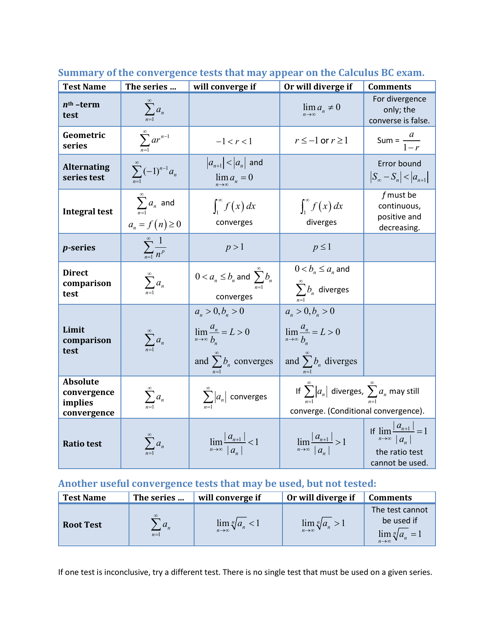
The Calculus BC Exam Series Convergence Tests Cheat Sheet is a resource that provides a condensed overview of the convergence tests used in calculus. It helps students in the Calculus BC course to understand and apply these tests when analyzing the convergence or divergence of a series.

The College Board, which is responsible for administering the AP Calculus BC exam, does not provide any official cheat sheets for the series convergence tests. It is important to rely on what you have learned in your calculus class and consult your teacher for any additional resources.

FAQ

Q: What is a series convergence test?A: A series convergence test is a method used to determine whether a given series converges or diverges.

Q: What is the Cauchy convergence test?A: The Cauchy convergence test states that if the limit of the sequence of partial sums of a series exists and is finite, then the series converges.

Q: What is the ratio test?A: The ratio test is a convergence test that involves taking the limit of the ratio of consecutive terms in a series. If the limit is less than 1, the series converges; if it is greater than 1, the series diverges; and if it is equal to 1, the test is inconclusive.

Q: What is the root test?A: The root test is a convergence test that involves taking the limit of the nth root of the absolute value of the terms in a series. If the limit is less than 1, the series converges; if it is greater than 1, the series diverges; and if it is equal to 1, the test is inconclusive.

Q: What is the integral test?A: The integral test is a convergence test that compares the sum of a series to the integral of a function. If the integral converges, the series converges; if the integral diverges, the series diverges.

Q: What is the alternating series test?A: The alternating series test is a convergence test used for alternating series. It states that if the terms of an alternating series decrease in absolute value and approach zero, then the series converges.

Q: What is the divergence test?A: The divergence test states that if the limit of the terms of a series does not approach zero, then the series diverges.

Q: What is the comparison test?A: The comparison test is a convergence test that compares the terms of a given series to the terms of a known convergent or divergent series. If the terms are similar, then the given series has the same convergence behavior.

Q: What is the limit comparison test?A: The limit comparison test is a convergence test that compares the terms of a given series to the terms of a known convergent series. If the limit of the ratio between the terms is a positive finite number, then the given series has the same convergence behavior as the known series.

Q: What is the absolute convergence test?A: The absolute convergence test states that if the sum of the absolute values of the terms in a series converges, then the series itself converges.