Math Proofs Cheat Sheet - Harold Toomey

FAQ

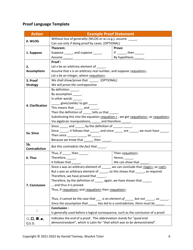
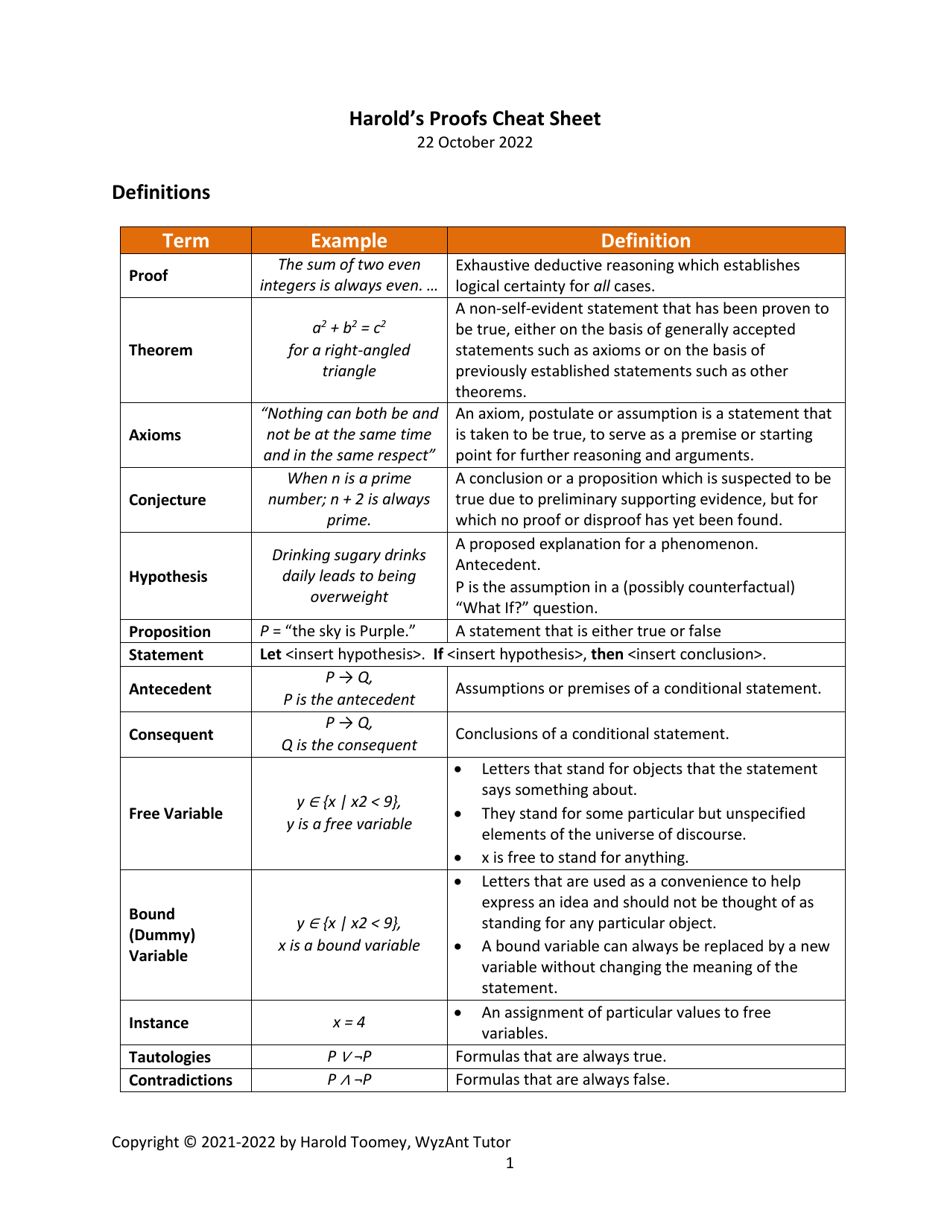
Q: What is a math proof?
A: A math proof is a logical argument that shows the validity of a mathematical statement.

Q: Why do we use math proofs?
A: Math proofs are used to establish the truth or validity of mathematical statements.

Q: What are some common proof techniques?
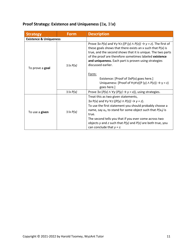
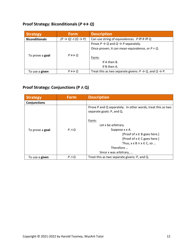
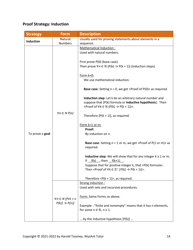
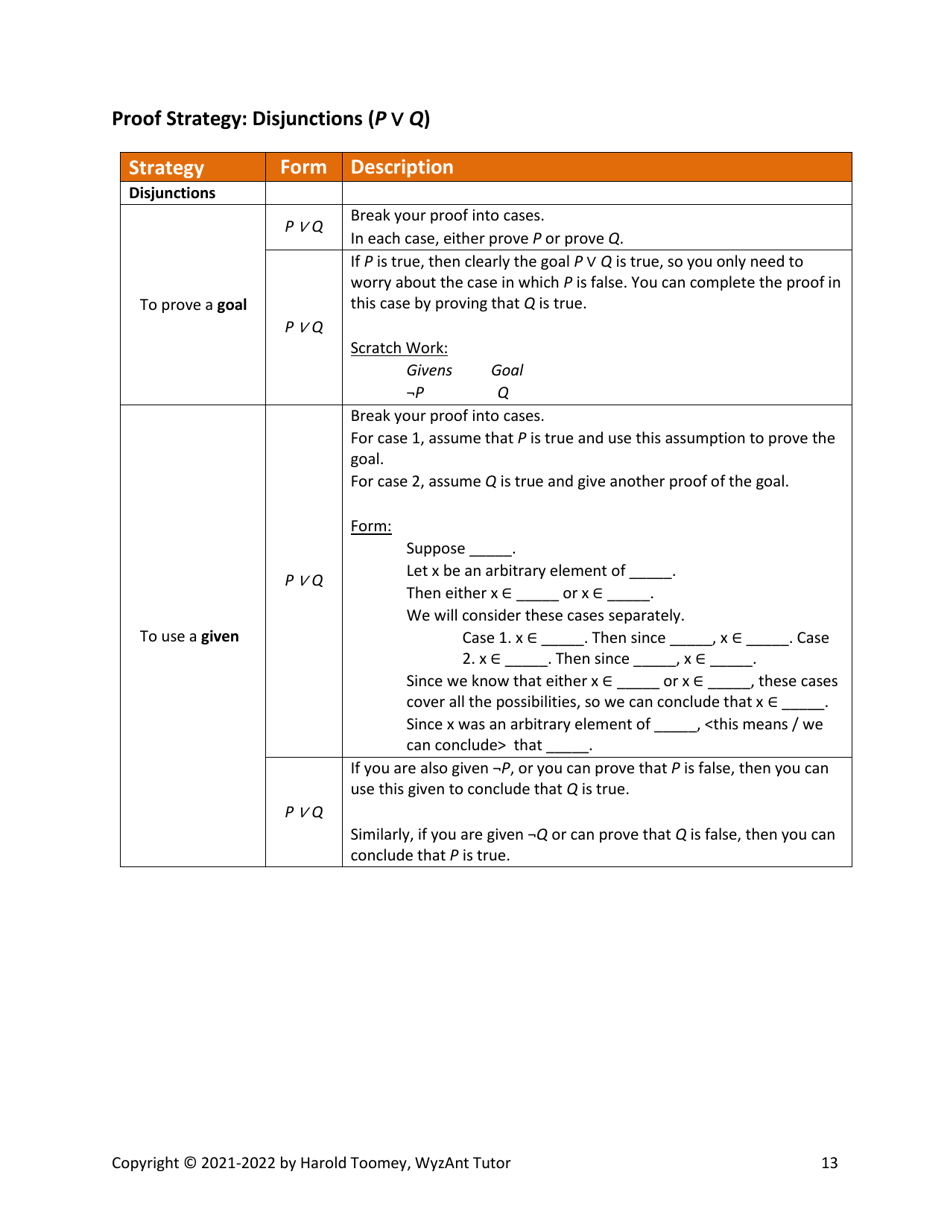
A: Some common proof techniques include direct proof, proof by contradiction, and proof by induction.

Q: How do you write a direct proof?
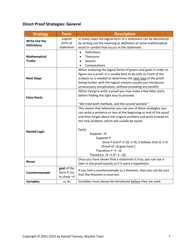
A: In a direct proof, you start with the given information and apply logical steps to arrive at the desired conclusion.

Q: What is proof by contradiction?
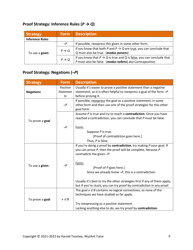
A: Proof by contradiction is a technique where you assume the opposite of the statement to be proved and show that it leads to a contradiction.

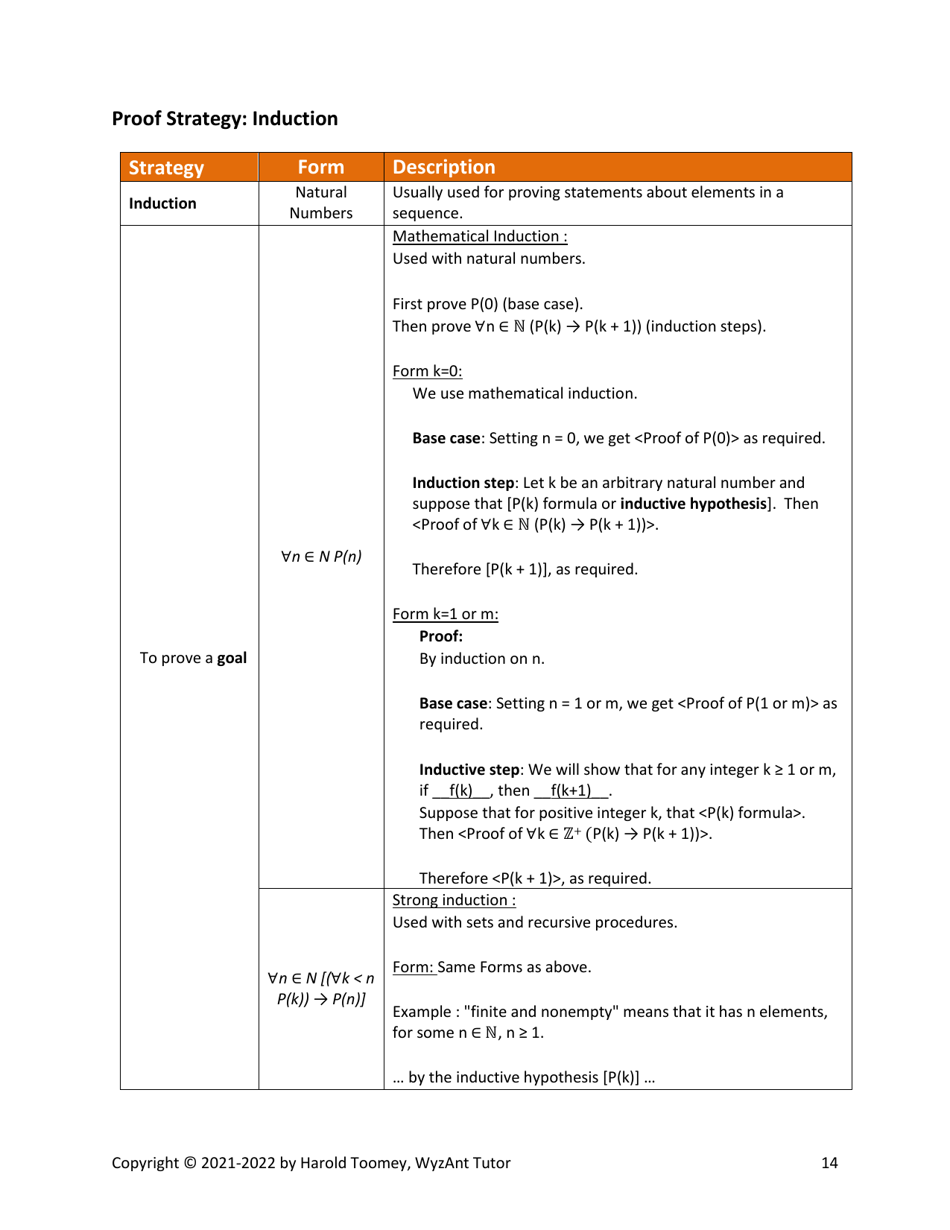
Q: What is proof by induction?
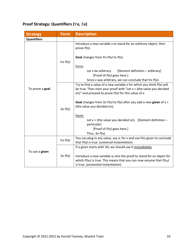
A: Proof by induction is a technique used to prove statements that depend on a variable, usually done in two steps: the base case and the induction step.

Q: What is the importance of rigor in math proofs?
A: Rigor ensures that a proof is logically sound and correctly demonstrates the truth or validity of a mathematical statement.

Q: Are math proofs always necessary?
A: In some cases, math proofs may not be needed, especially for simple and well-known results. However, they are essential for establishing new mathematical truths.

Q: Can anyone write a math proof?
A: Writing a math proof requires knowledge of mathematical concepts and logical reasoning skills. While anyone can learn to write proofs, it may take practice and understanding.