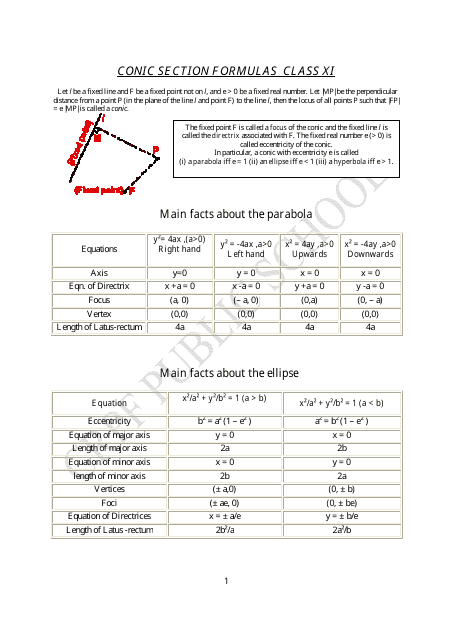
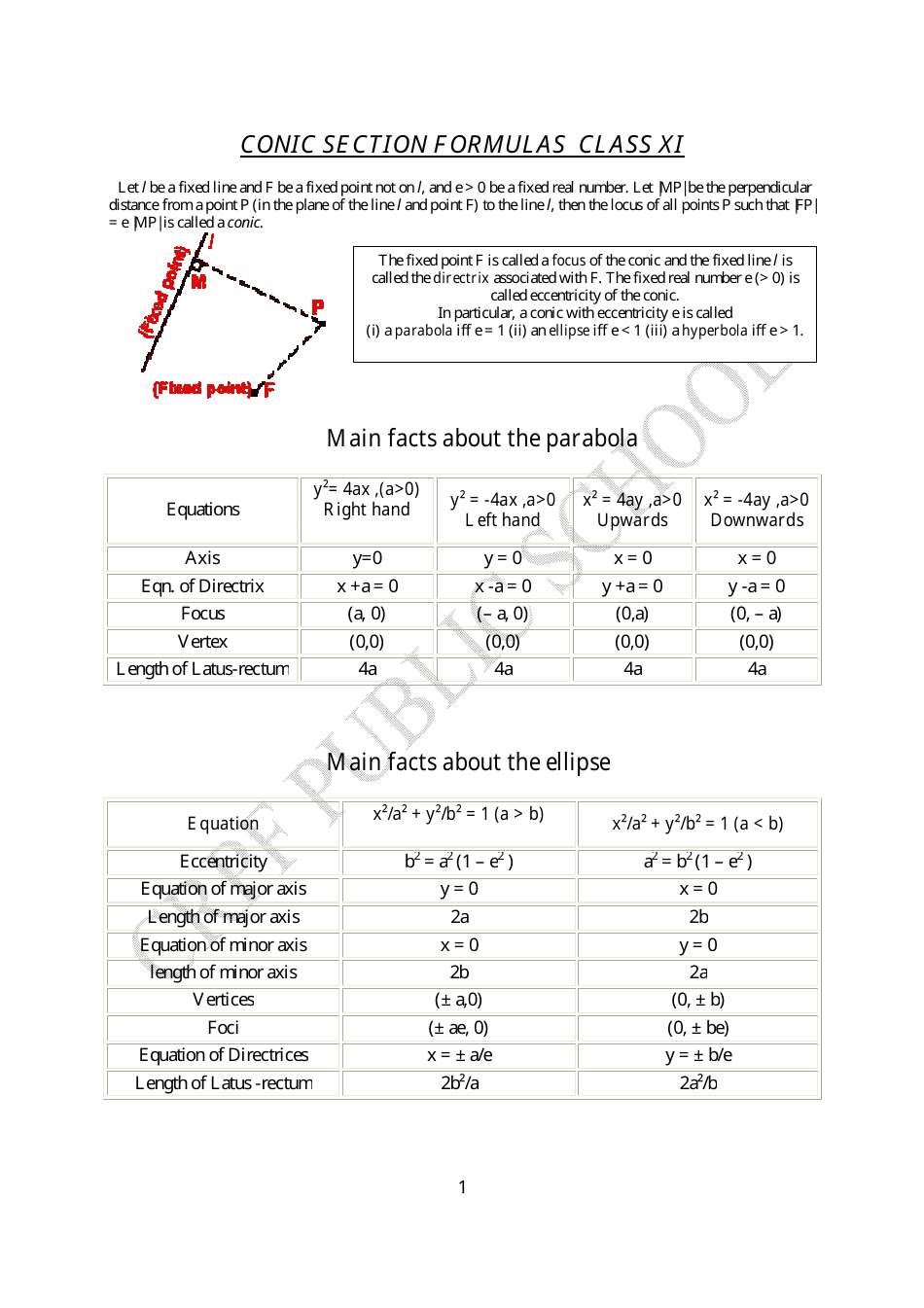
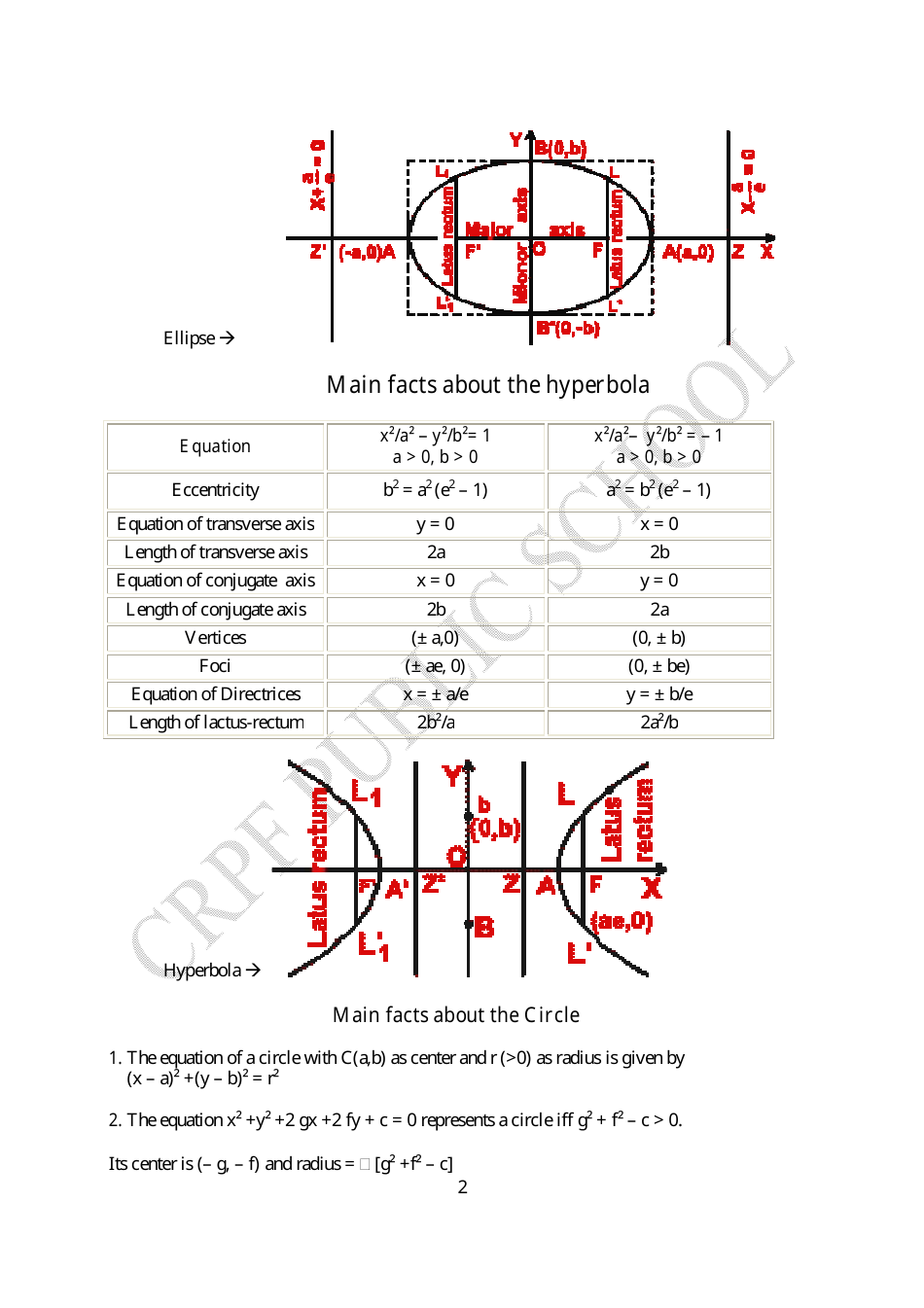
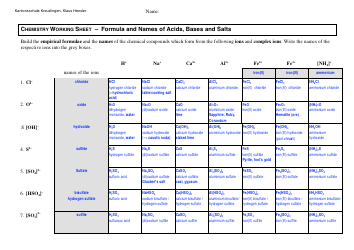
Conic Section Formulas Cheat Sheet

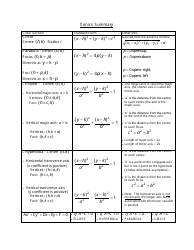
The Conic Section Formulas Cheat Sheet is a useful reference tool that provides formulas for conic sections such as circles, ellipses, parabolas, and hyperbolas. It helps individuals solve mathematical problems related to these curves.

The Conic Section Formulas Cheat Sheet is typically filed by individuals or organizations who create and distribute such educational materials.

FAQ

Q: What is a conic section?
A: A conic section is a curve that can be obtained as the intersection of a cone with a plane.

Q: What are the different types of conic sections?
A: The different types of conic sections are: the circle, ellipse, parabola, and hyperbola.

Q: What is the general equation for a conic section?
A: The general equation for a conic section is: Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0.

Q: What is the equation for a circle?
A: The equation for a circle is: (x - h)^2 + (y - k)^2 = r^2, where (h, k) is the center of the circle and r is the radius.

Q: What is the equation for an ellipse?
A: The equation for an ellipse is: (x - h)^2/a^2 + (y - k)^2/b^2 = 1, where (h, k) is the center of the ellipse, a is the horizontal radius, and b is the vertical radius.

Q: What is the equation for a parabola?
A: The equation for a parabola is: y = ax^2 + bx + c, where a, b, and c are constants.

Q: What is the equation for a hyperbola?
A: The equation for a hyperbola is: (x - h)^2/a^2 - (y - k)^2/b^2 = 1, where (h, k) is the center of the hyperbola, a is the horizontal radius, and b is the vertical radius.