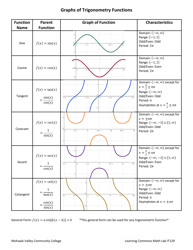
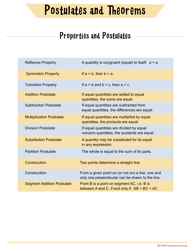
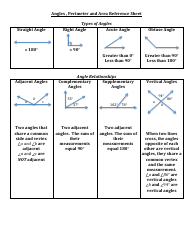
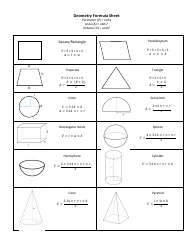
Linear Algebra Summary Cheat Sheet

A Linear Algebra Summary Cheat Sheet is a condensed resource that provides an overview of key concepts, formulas, and techniques used in the field of linear algebra. It is used as a quick reference guide for students and professionals to review or refresh their understanding of linear algebra topics.

FAQ

Q: What is linear algebra?
A: Linear algebra is a branch of mathematics that deals with vectors, vector spaces, linear transformations, and systems of linear equations.

Q: Why is linear algebra important?
A: Linear algebra is used in various fields such as computer science, engineering, physics, and data analysis. It provides a framework for solving complex mathematical problems.

Q: What are vectors?
A: Vectors are mathematical objects that have both magnitude and direction. They can be represented as arrows or ordered lists of numbers.

Q: What is a vector space?
A: A vector space is a set of vectors that satisfy certain properties, such as closure under addition and scalar multiplication.

Q: What are linear transformations?
A: Linear transformations are functions that map one vector space to another, while preserving the structure of the vector space.

Q: What are systems of linear equations?
A: Systems of linear equations are collections of equations involving linear terms. They can be solved using techniques such as Gaussian elimination or matrix inversion.

Q: What is a matrix?
A: A matrix is a rectangular array of numbers. It can represent a system of linear equations or a linear transformation.

Q: What is the determinant of a matrix?
A: The determinant of a square matrix is a value that provides information about the matrix's invertibility and the scaling factor of the linear transformation it represents.

Q: What is eigenvalue and eigenvector?
A: Eigenvalues and eigenvectors are concepts used to study the behavior of a linear transformation. An eigenvector is a non-zero vector that is only scaled by a linear transformation, while the corresponding eigenvalue represents the scaling factor.

Q: What is diagonalization?
A: Diagonalization is the process of representing a matrix as a diagonal matrix using its eigenvectors and eigenvalues.