Trigonometric Substitution Cheat Sheet

The Trigonometric Substitution Cheat Sheet is a document that provides a quick reference guide for tackling integrals involving trigonometric functions using substitution techniques. It helps users understand and apply the appropriate trigonometric substitutions to simplify and solve integrals effectively.

FAQ

Q: What is trigonometric substitution?A: Trigonometric substitution is a technique used in calculus to simplify integrals or solve problems involving trigonometric functions.

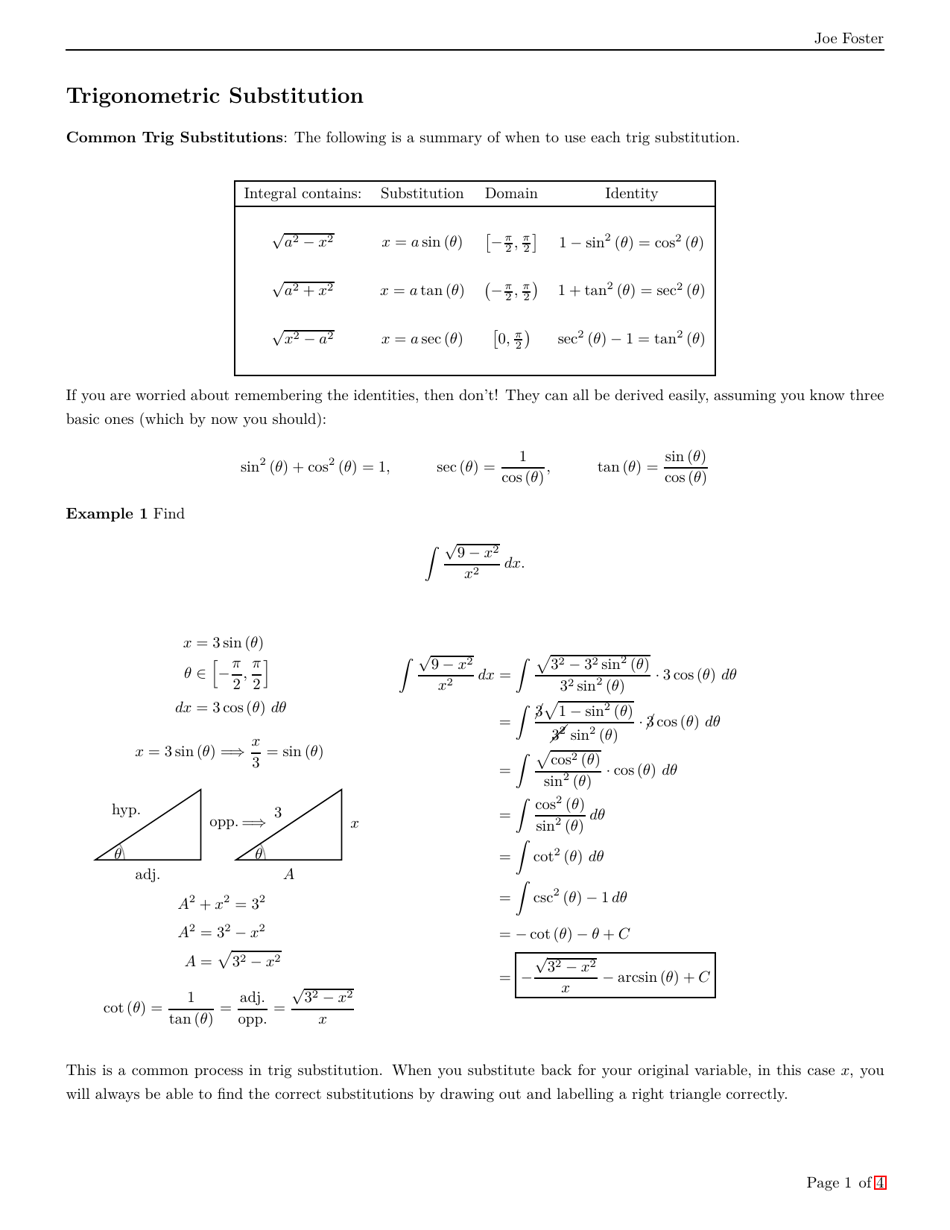
Q: When is trigonometric substitution used?A: Trigonometric substitution is used when the integrand contains a square root of the form sqrt(a^2 - x^2), sqrt(x^2 - a^2), or sqrt(x^2 + a^2) where a is a constant.

Q: What are the common trigonometric substitutions?A: The common trigonometric substitutions include substituting x with sin(theta), cos(theta), or tan(theta) to simplify the integral.

Q: How do you choose the appropriate trigonometric substitution?A: To choose the appropriate trigonometric substitution, you should look for a square root expression and identify it as one of the three forms mentioned earlier.

Q: What are the trigonometric identities used in trigonometric substitution?A: The trigonometric identities used in trigonometric substitution include sin^2(theta) + cos^2(theta) = 1, tan^2(theta) + 1 = sec^2(theta), and 1 + cot^2(theta) = csc^2(theta).

Q: What is the purpose of trigonometric substitution?A: The purpose of trigonometric substitution is to replace the variable in an integral with a trigonometric function that simplifies the integral and makes it easier to evaluate.