Big O Notation Cheat Sheet

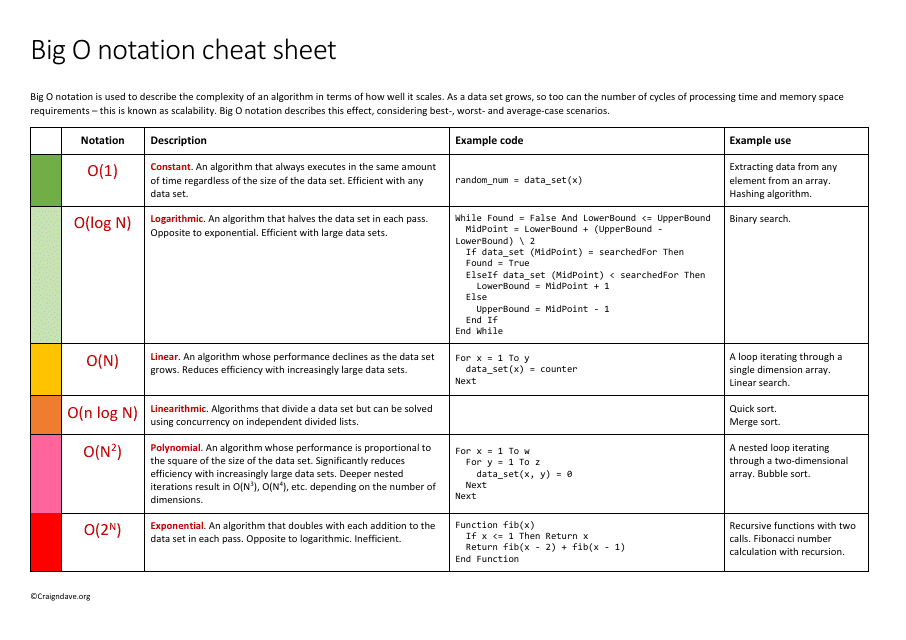
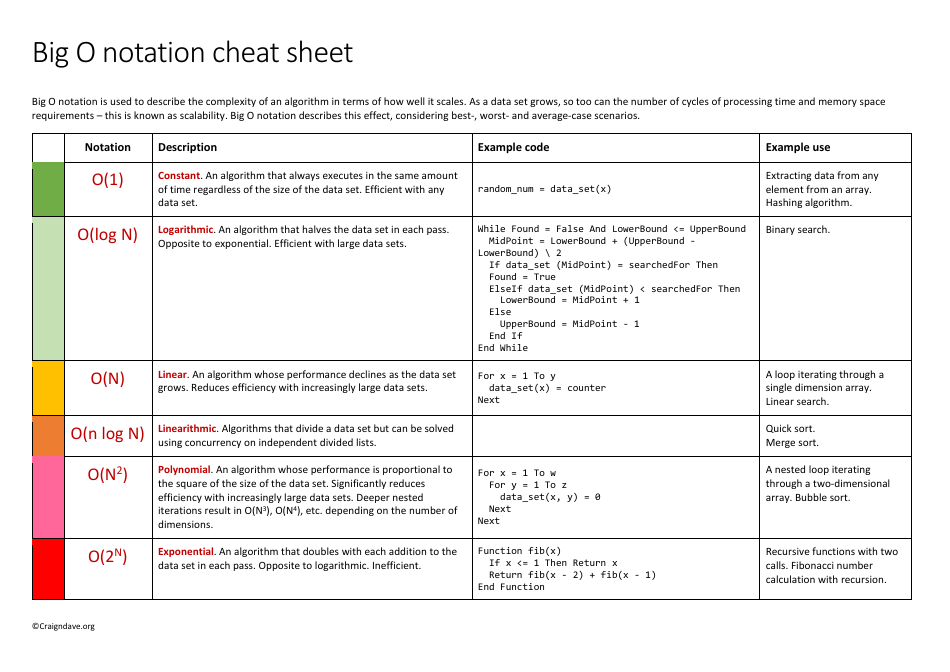
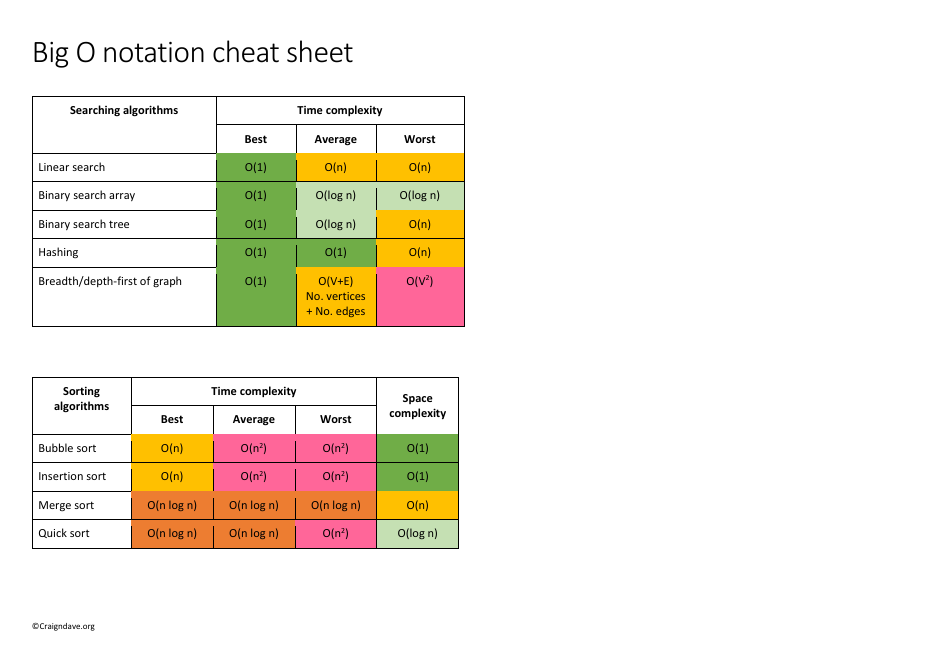
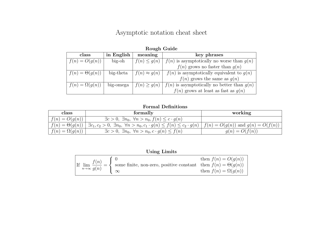
The Big O Notation Cheat Sheet is a reference guide used in computer science and programming to analyze the efficiency of algorithms. It helps developers understand the performance characteristics of an algorithm by describing how the algorithm's runtime or space requirements grow as the input size increases. It provides a quick overview of different time complexity classes (such as O(1), O(log n), O(n), etc.) and their corresponding growth rates.

FAQ

Q: What is Big O notation?A: Big O notation is a way to describe the time complexity of an algorithm.

Q: Why is Big O notation important?A: Big O notation helps us analyze the efficiency of an algorithm and compare different algorithms.

Q: What does O(1) mean in Big O notation?A: O(1) means that the algorithm's time complexity is constant, meaning it takes the same amount of time regardless of the input size.

Q: What does O(n) mean in Big O notation?A: O(n) means that the algorithm's time complexity is linear, meaning the time it takes grows linearly with the size of the input.

Q: What does O(log n) mean in Big O notation?A: O(log n) means that the algorithm's time complexity grows logarithmically with the input size, which is generally more efficient than linear.

Q: What does O(n^2) mean in Big O notation?A: O(n^2) means that the algorithm's time complexity is quadratic, meaning the time it takes grows exponentially with the size of the input.

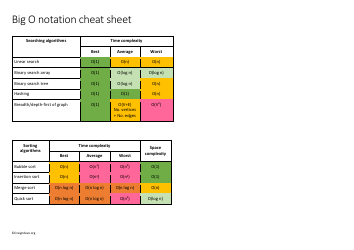
Q: What is the best case scenario in Big O notation?A: The best case scenario represents the lower bound of the algorithm's time complexity, meaning the best possible time it can take.

Q: What is the worst case scenario in Big O notation?A: The worst case scenario represents the upper bound of the algorithm's time complexity, meaning the maximum time it can take.

Q: What is the average case scenario in Big O notation?A: The average case scenario represents the average time complexity of the algorithm, taking into account different inputs and probabilities.

Q: Can Big O notation be used to measure space complexity?A: Yes, Big O notation can also be used to describe the space complexity of an algorithm, indicating how much memory it requires.