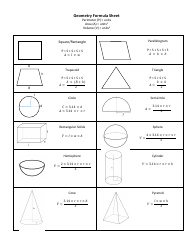
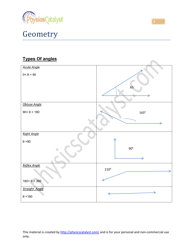
Math Cheat Sheet - Logs and Exponentials

A Math Cheat Sheet for Logs and Exponentials is a reference document that provides formulas, rules, and examples related to logarithms and exponential functions. It is a handy tool for students and anyone studying or working with these mathematical concepts.

FAQ

Q: What is a logarithm?
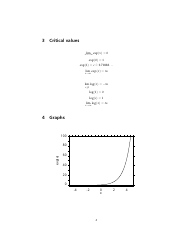
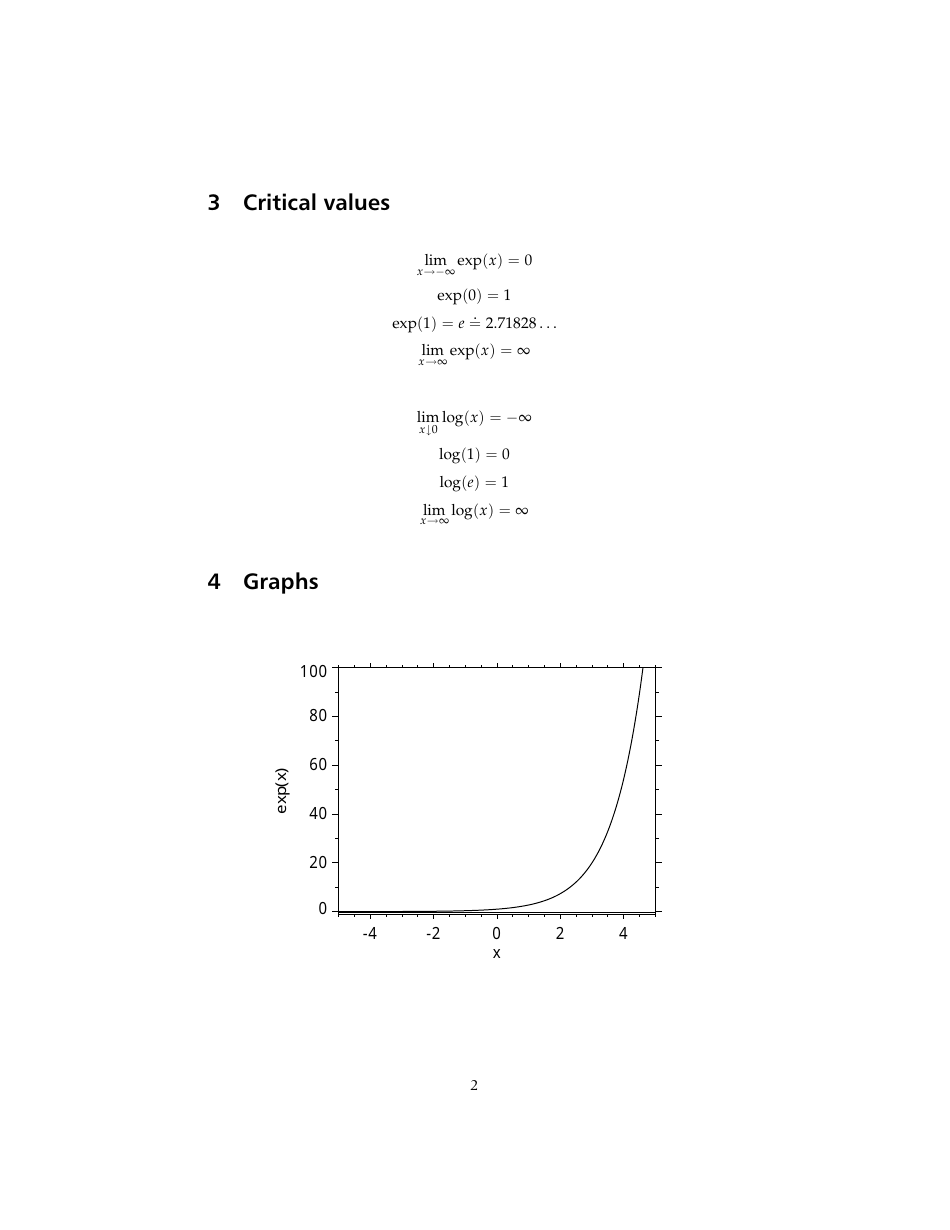
A: A logarithm is the inverse operation of exponentiation. It tells you what power you need to raise a specific base to in order to get a certain number.

Q: What is the natural logarithm?
A: The natural logarithm, denoted as ln, is a logarithm with the base e (Euler's number, approximately 2.71828).

Q: What is exponential notation?
A: Exponential notation is a way of representing repeated multiplication with a base number and an exponent.

Q: What is the rule for multiplying exponential numbers?
A: When multiplying exponential numbers with the same base, you add the exponents.

Q: What is the rule for dividing exponential numbers?
A: When dividing exponential numbers with the same base, you subtract the exponent of the divisor from the exponent of the dividend.

Q: What is the rule for raising exponential numbers to a power?
A: When raising exponential numbers to a power, you multiply the exponents.

Q: What is a common logarithm?
A: A common logarithm, denoted as log, is a logarithm with the base 10.

Q: What is the property of logarithms that allows you to combine two logarithms with the same base?
A: The property is called the logarithmic identity. It states that log base a x + log base a y = log base a (x * y).

Q: What is the property of logarithms that allows you to separate a logarithm of a product into the sum of two logarithms?
A: The property is called the logarithmic product rule. It states that log base a (x * y) = log base a x + log base a y.

Q: What is the property of logarithms that allows you to separate a logarithm of a quotient into the difference of two logarithms?
A: The property is called the logarithmic quotient rule. It states that log base a (x / y) = log base a x - log base a y.