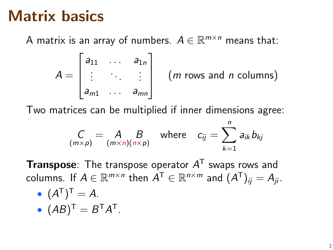Linear Algebra Cheat Sheet - University of Wisconsin-Madison

A Linear Algebra Cheat Sheet is a condensed reference guide that contains key formulas, concepts, and techniques used in Linear Algebra. It can be used as a quick reference tool for students, professionals, or anyone studying or working in the field of mathematics, engineering, computer science, or any other discipline that utilizes Linear Algebra.

FAQ

Q: What is linear algebra?
A: Linear algebra is a branch of mathematics that deals with vector spaces and linear equations.

Q: What are vectors?
A: Vectors are mathematical objects that represent both magnitude and direction.

Q: What are matrices?
A: Matrices are rectangular arrays of numbers or symbols, arranged in rows and columns.

Q: What is a system of linear equations?
A: A system of linear equations is a set of equations that can be written in the form Ax = b, where A is a matrix, x is a column vector of variables, and b is a column vector of constants.

Q: What is a determinant?
A: A determinant is a scalar value that can be computed for a square matrix, representing certain properties of the matrix.

Q: What is a vector space?
A: A vector space is a collection of vectors that satisfy certain properties, such as closure under addition and scalar multiplication.

Q: What is the rank of a matrix?
A: The rank of a matrix is the maximum number of linearly independent rows or columns in the matrix.

Q: What is eigenvalue and eigenvector?
A: An eigenvector is a non-zero vector that remains unchanged when a linear transformation is applied to it, and the corresponding eigenvalue is the scalar value associated with that eigenvector.