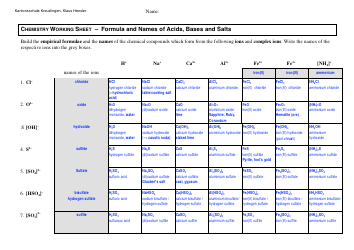
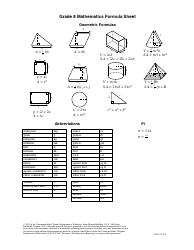
Conics Formula Cheat Sheet

The Conics Formula Cheat Sheet is a document that provides a quick reference for formulas and equations used in conics, which is a branch of mathematics that deals with curves and shapes like circles, ellipses, parabolas, and hyperbolas. It can be helpful for students and professionals studying or working with conics in various fields such as physics, engineering, and mathematics.

The Conics Formula Cheat Sheet is typically created and filed by students or teachers who use it as a reference for studying conic sections in mathematics.

FAQ

Q: What is a conic?
A: A conic is a curve that can be formed by the intersection of a plane with a double-napped cone.

Q: What are the different types of conics?
A: The different types of conics are circles, ellipses, parabolas, and hyperbolas.

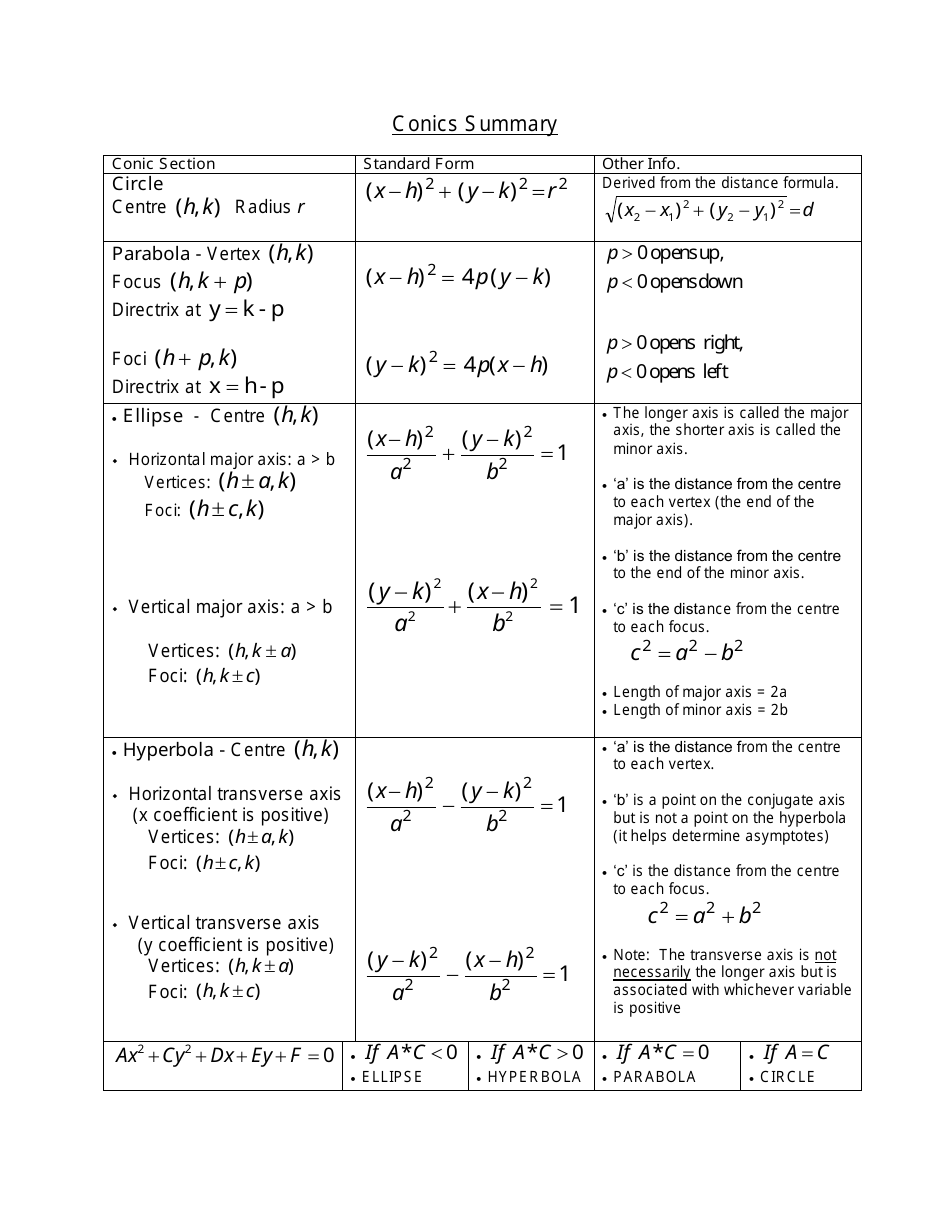
Q: What is the standard form of a circle equation?
A: The standard form of a circle equation is (x - h)^2 + (y - k)^2 = r^2, where (h, k) represents the center of the circle and r represents the radius.

Q: What is the standard form of an ellipse equation?
A: The standard form of an ellipse equation is (x - h)^2 / a^2 + (y - k)^2 / b^2 = 1, where (h, k) represents the center of the ellipse and a and b represent the semi-major and semi-minor axes, respectively.

Q: What is the standard form of a parabola equation?
A: The standard form of a parabola equation is y = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola and a determines the direction and shape of the curve.

Q: What is the standard form of a hyperbola equation?
A: The standard form of a hyperbola equation is (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1, where (h, k) represents the center of the hyperbola and a and b determine the size and shape of the curve.

Q: What is the focus-directrix property of a conic?
A: The focus-directrix property states that for every point on a conic, the distance to the focus is equal to the distance to the directrix.