Graphing Quadratic Functions in Vertex Form Practice Worksheet With Answers

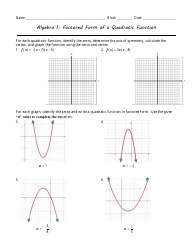
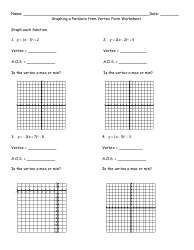
A Graphing Quadratic Functions in Vertex Form Practice Worksheet with Answers is typically used by students to practice analyzing and graphing quadratic functions in vertex form. It helps them understand the concepts and techniques involved in graphing these functions.

The practice worksheet with answers for graphing quadratic functions in vertex form is typically filed by individual students or teachers in educational institutions.

FAQ

Q: What is the vertex form of a quadratic function?
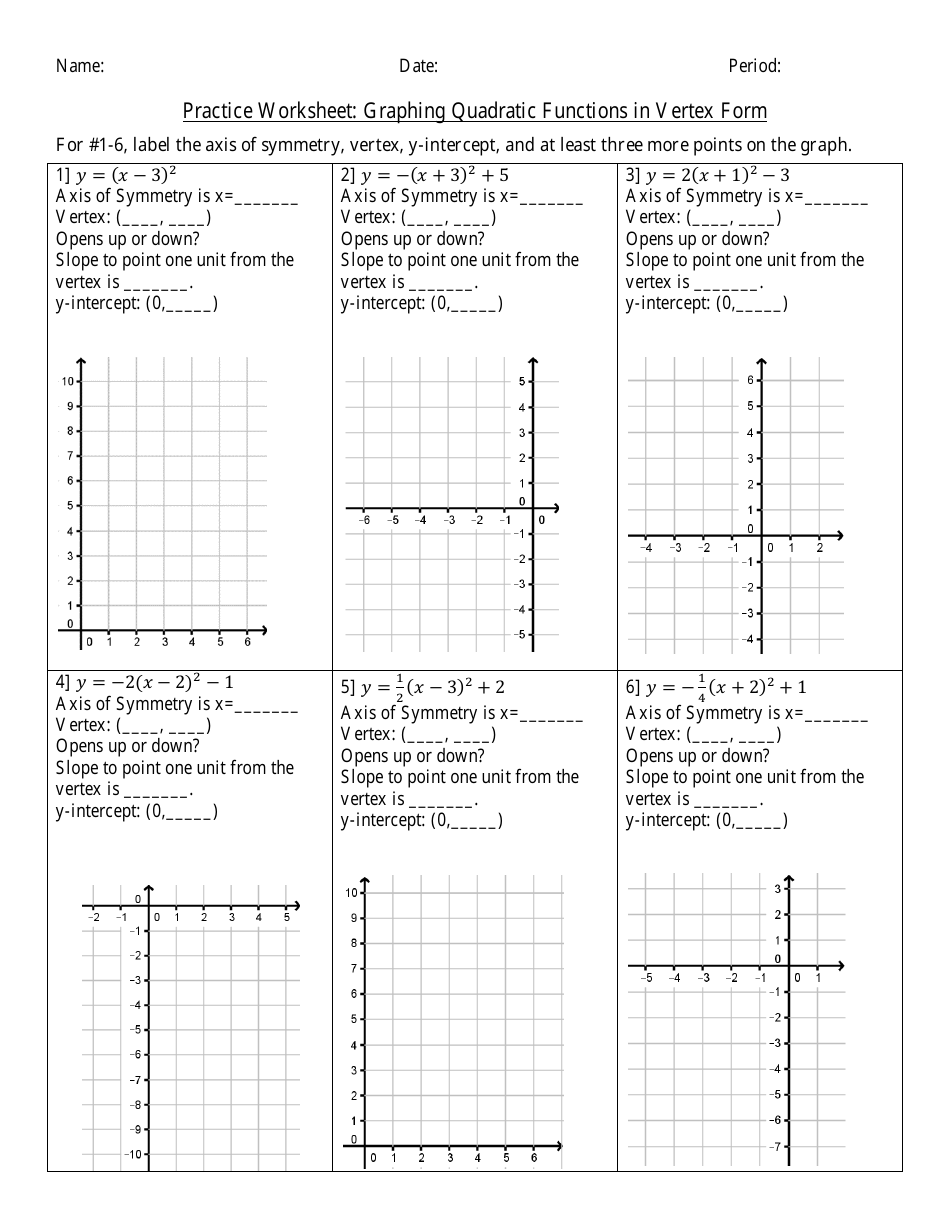
A: The vertex form of a quadratic function is y = a(x-h)^2 + k, where (h, k) represents the vertex of the parabola.

Q: How do you graph a quadratic function in vertex form?
A: To graph a quadratic function in vertex form, plot the vertex (h, k), and use the symmetry of the parabola to plot two additional points on either side of the vertex.

Q: How do you find the vertex of a quadratic function given in vertex form?
A: The vertex of a quadratic function given in vertex form is (h, k), where h is the x-coordinate of the vertex and k is the y-coordinate of the vertex.

Q: What does the 'a' term represent in the vertex form of a quadratic function?
A: The 'a' term in the vertex form of a quadratic function represents the stretch or compression factor of the parabola.

Q: How do you determine whether a quadratic function opens upward or downward based on the 'a' term?
A: If the 'a' term is positive, the quadratic function opens upward. If the 'a' term is negative, the quadratic function opens downward.