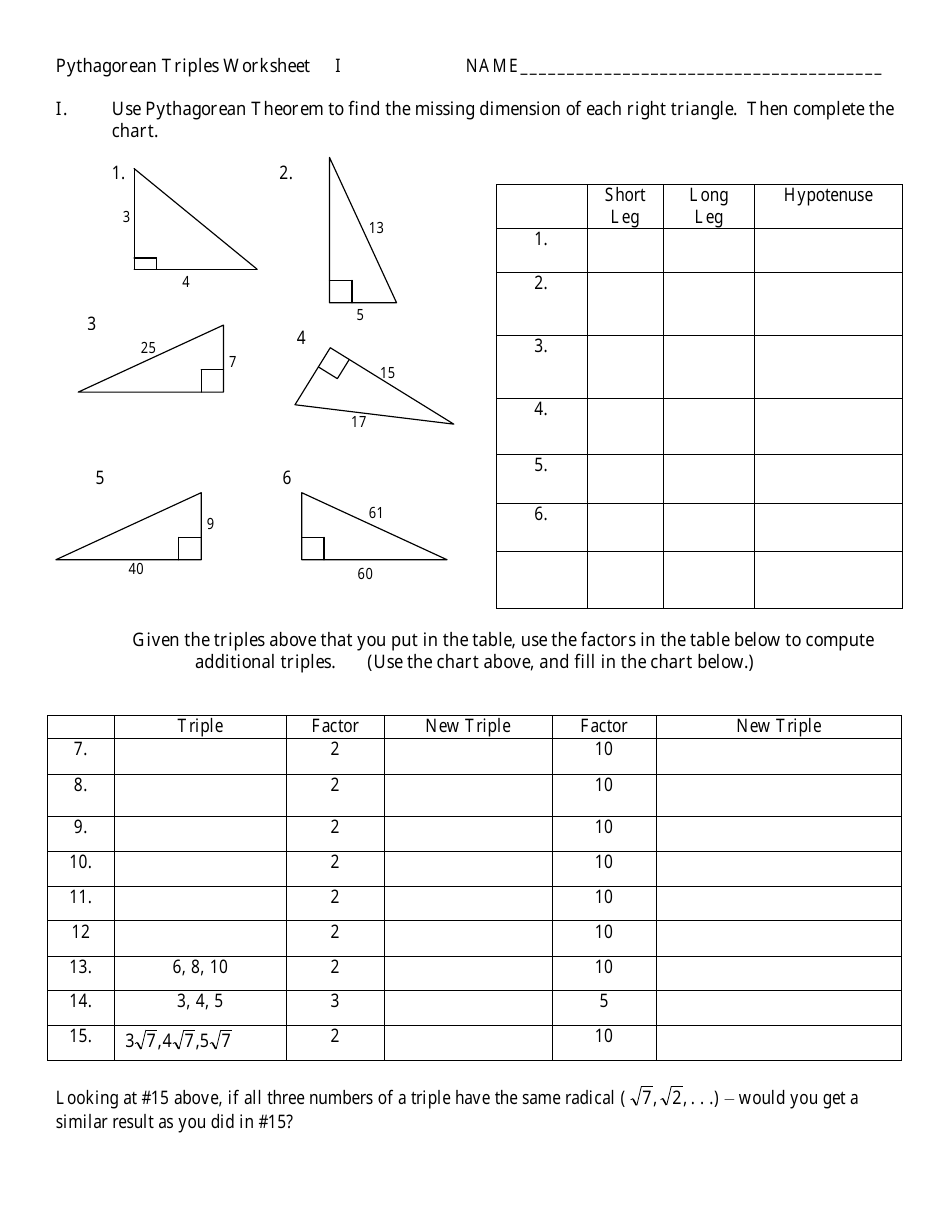
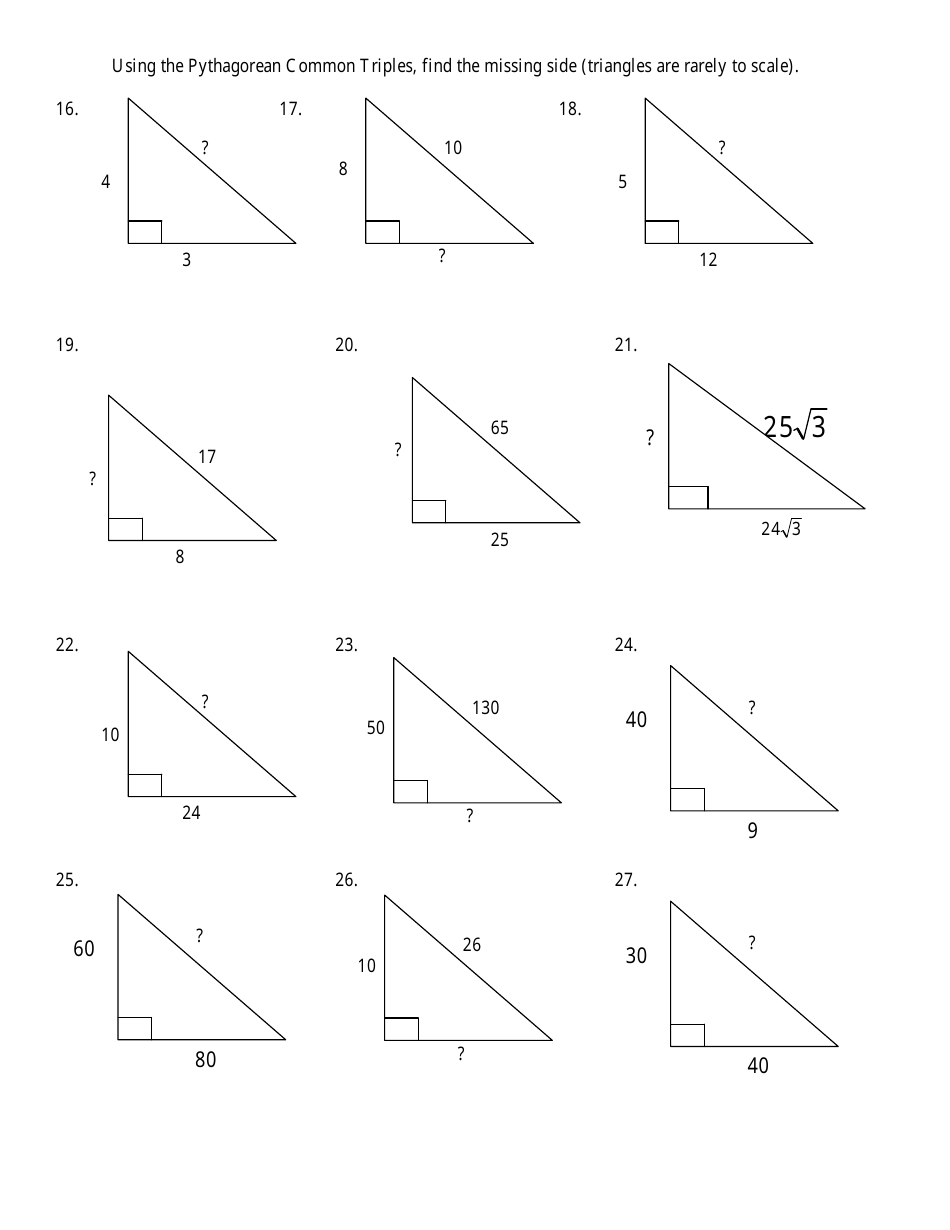
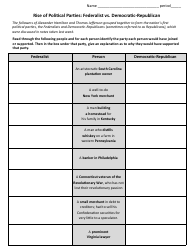
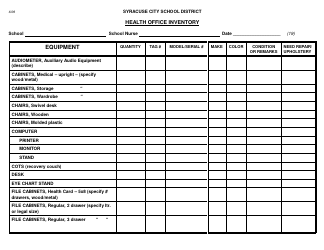
Pythagorean Triples Worksheet - West Ada School District

The Pythagorean Triples Worksheet is a resource provided by the West Ada School District for students to practice solving problems involving Pythagorean triples. It helps them understand and apply the Pythagorean theorem, which is a fundamental concept in geometry.

FAQ

Q: What is a Pythagorean triple?A: A Pythagorean triple is a set of three positive integers that satisfy the Pythagorean theorem: a^2 + b^2 = c^2.

Q: What is the Pythagorean theorem?A: The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.

Q: What are some examples of Pythagorean triples?A: Examples of Pythagorean triples include (3, 4, 5), (5, 12, 13), and (8, 15, 17).

Q: How can Pythagorean triples be generated?A: Pythagorean triples can be generated using the formulas: a = m^2 - n^2, b = 2mn, and c = m^2 + n^2, where m and n are positive integers.

Q: What is the importance of Pythagorean triples?A: Pythagorean triples are important in geometry and mathematics because they represent the side lengths of right triangles, which have many practical and theoretical applications.

Q: How can Pythagorean triples be used in real life?A: Pythagorean triples are used in fields such as architecture, engineering, and construction to calculate the length of diagonal or hypotenuse in right-angled structures.

Q: Are there any special properties of Pythagorean triples?A: Yes, some special properties of Pythagorean triples include: a Pythagorean triple is always a multiple of another Pythagorean triple, and all Pythagorean triples are either odd-odd-odd or even-even-even.

Q: Is there a limit to the size of Pythagorean triples?A: No, there is no limit to the size of Pythagorean triples. As long as the values of m and n satisfy the conditions, Pythagorean triples can have arbitrarily large numbers.

Q: Can Pythagorean triples have negative numbers?A: No, Pythagorean triples are defined to have positive integer values for the sides of the right triangle, so negative numbers are not considered as part of a Pythagorean triple.