Creating Equivalent Ratios Worksheet With Answer Key

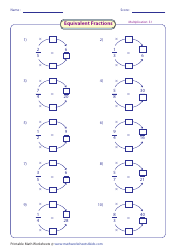
A Creating Equivalent Ratios Worksheet with Answer Key is typically used in educational settings, such as classrooms or tutoring sessions, to help students practice their skills in creating equivalent ratios. This worksheet provides a series of ratio problems that students must solve by finding equivalent ratios. The answer key is included to allow students to check their work and verify their solutions. By working through this worksheet, students will gain a better understanding of ratios and the concept of equivalence. This practice helps them build their math skills and prepares them for more advanced mathematical concepts.

The Creating Equivalent Ratios Worksheet with Answer Key is typically filed by the individual or organization responsible for creating and distributing the worksheet. This could be a teacher, a textbook publisher, or an educational website, among others. It is not filed with any specific authority or government entity.

FAQ

Q: What is an equivalent ratio?
A: An equivalent ratio is a ratio that has the same value as another ratio, even though the numbers may be different.

Q: How do you create an equivalent ratio?
A: To create an equivalent ratio, you need to multiply or divide both parts of the ratio by the same number.

Q: Why are equivalent ratios important?
A: Equivalent ratios are important because they allow us to compare quantities and solve problems involving ratios more easily. They help us understand the relationship between different quantities in a ratio.

Q: Can you provide an example of creating an equivalent ratio?
A: Sure! Let's say we have the ratio 2:3. To create an equivalent ratio, we can multiply both parts of the ratio by 2. The equivalent ratio would be 4:6.

Q: How can you check if two ratios are equivalent?
A: To check if two ratios are equivalent, you can simplify them. If the simplified form of both ratios is the same, then they are equivalent.

Q: What is a simplified form of a ratio?
A: A simplified form of a ratio is when both parts of the ratio have been divided by their greatest common factor (GCF). It is the ratio reduced to its simplest form.

Q: Can you simplify the ratio 16:24?
A: Yes, to simplify the ratio 16:24, we divide both parts by their greatest common factor, which is 8. The simplified ratio is 2:3.

Q: How can you use equivalent ratios to solve a problem?
A: You can use equivalent ratios to solve a problem by setting up proportions. Once you have a proportion, you can cross-multiply and solve for the unknown quantity.

Q: What is a proportion?
A: A proportion is an equation that states that two ratios are equal. It is often used to solve problems involving ratios.

Q: Can you provide an example of solving a problem using equivalent ratios?
A: Of course! Let's say we have a recipe that calls for 3 cups of flour and 2 eggs, but we want to make a larger batch. If we know that the recipe is equivalent to the ratio 6:4, we can use this information to calculate the amount of flour and eggs needed for the larger batch.