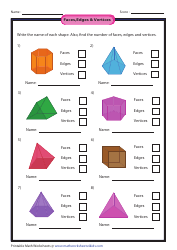
Faces, Edges & Vertices Worksheet With Answer Key - Book

The Faces, Edges & Vertices Worksheet With Answer Key - Book is used as a learning resource to help students understand and practice the concepts of faces, edges, and vertices in geometry. It provides worksheets and an answer key to support learning and evaluate progress.

FAQ

Q: What are faces, edges, and vertices?
A: Faces are the flat sides of a 3D shape, edges are the lines where the faces meet, and vertices are the points where the edges meet.

Q: How are faces, edges, and vertices related?
A: Faces, edges, and vertices are all parts of a 3D shape and help define its structure.

Q: What is the difference between a face and an edge?
A: A face is a flat surface, while an edge is a line where two faces meet.

Q: What is the difference between an edge and a vertex?
A: An edge is a line where two faces meet, while a vertex is a point where multiple edges meet.

Q: Give an example of a shape with 6 faces, 12 edges, and 8 vertices.
A: A cube has 6 faces, 12 edges, and 8 vertices.

Q: What is the formula for Euler's polyhedron formula?
A: The formula is V + F - E = 2, where V represents the number of vertices, F represents the number of faces, and E represents the number of edges of a 3D shape.

Q: Why is Euler's polyhedron formula important?
A: Euler's polyhedron formula is important because it relates the number of faces, vertices, and edges of a 3D shape and helps verify its topological properties.

Q: How can I use faces, edges, and vertices to identify a 3D shape?
A: By counting the number of faces, edges, and vertices of a 3D shape, you can identify its specific type.

Q: Are faces, edges, and vertices only relevant to 3D shapes?
A: Yes, faces, edges, and vertices are characteristics specific to 3D shapes.

Q: What is the purpose of a worksheet on faces, edges, and vertices?
A: A worksheet on faces, edges, and vertices helps reinforce understanding and practice skills related to identifying and counting these features in 3D shapes.